Для апробации своей физической модели занимаюсь решением на её основе топовых задач физики. Одна из них - аномальное смещение перигелия Меркурия. Формулу для нее нашел Пауль Гербер в 1898 году. Поскольку в формулу вошла скорость света, то он решил, что гравитация распространяется со скоростью света. В 1915 году Эйнштейн получил в точности такую же формулу в рамках ОТО, связав скорость света в ней с гравитационным радиусом Солнца.
Когда я решил эту задачу, пользуясь своею моделью, конечно же сравнил с тем, как это сделали Гербер и Эйнштейн.
Как это выглядит у Эйнштейна
за один оборот, где
- угол аномального смещения перигелия.
Один оборот это .
Тогда удобнее формулу переписать так:
то есть дробь - есть малое число, указывающее на часть от угла в .
Теперь обратите внимание на то, что в знаменателе имеется квадрат скорости света. Следовательно выражение тоже должно иметь размерность квадрата скорости, чтобы дробь оставалась безразмерной.
Квадрат орбитальной скорости имеет очень похожий вид: , где
- истинная аномалия (угол между направлением на перицентр из центра Солнца и радиус вектором тела на орбите, отсчитывается против часовой стрелки).
Первый знак "+" внутри скобки означает, что Солнце находится в правом фокусе эллипса орбиты, а сам эллипс расположен "горизонтально", т.е. большая полуось - горизонтальна.
Теперь видно, что тройка Гербера-Эйнштейна приравнивается к этой скобке: (*)
Чем же так отличается тройка? Или, чем так отличаются истинные аномалии тел на орбите?
Из (*) следует, что
Поскольку эксцентриситеты орбит для небесных тел известны, вычислим, какие углы обусловлены "тройкой".
Оказывается - никакие. Дело в том, что для Меркурия, например, =4,7
Венера - =147, Земля
=60, Марс
=10,6
и только Икар =0,79 с истинной аномалией в 37 градусов.
Таким образом орбитальная привязка формулы Гербера-Эйнштейна не удалась.
Дальнейшее изложение не имеет связи с вышеприведенным лирическим отступлением.
Пользуясь своей моделью, получил формулу угловой добавки за один оборот:
, где V - некая орбитальная скорость тела вокруг гравитирующего центра. Неравномерное накопление аномального смещения перигелия на эллиптической орбите ведет себя так же, как равномерное накопление на круговой орбите с радиусом из расчета:
, где R - радиус круговой орбиты, a и b - большая и малая полуоси эллиптической орбиты.
Тогда .
Учитывая, что , где
- эксцентриситет эллипса,
- радиус круговой орбиты,
- скорость движения на круговой орбите.
Соответственно, для тела пересчитывается период обращения и количество оборотов за 100 лет.
Применялись, конечно, и другие виды расчетов.
Прямой расчет суммированием углов смещения перигелия на коротких участках орбиты. Угол истинной аномалии вычислялся по положению отрезка дуги эллипса. Скорость на этом участке дуги считалась неизменной. Весь эллипс орбиты разбивался на 360 таких участков, но для расчета достаточно половины эллипса от перигелия до афелия. Результат просто удваивался.
То есть, за один оборот:
Простое интегрирование не удалось. Интеграл эллиптический. 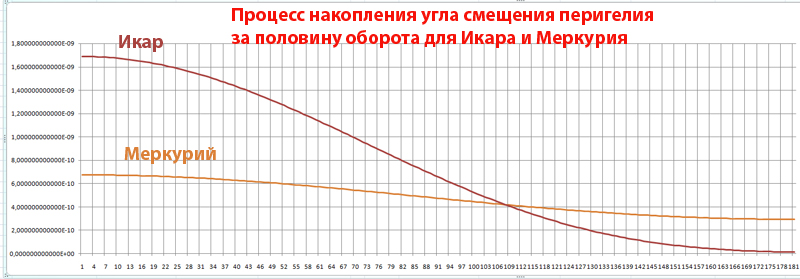 Несмотря на то, что Икар за один оборот набирает почти вдвое больший угол смещения перигелия, период его обращения 408 суток, у Меркурия всего 88 суток, поэтому за столетие Меркурий набирает гораздо большее смещение перигелия.
Несмотря на то, что Икар за один оборот набирает почти вдвое больший угол смещения перигелия, период его обращения 408 суток, у Меркурия всего 88 суток, поэтому за столетие Меркурий набирает гораздо большее смещение перигелия.
Таким образом в секундах дуги за столетие:
| Небесное тело | Эйнштейн | Наблюдение | Моё |
| Меркурий | 43,0 | 43,1 ± 0,5 | 44,3 |
| Венера | 8,6 | 8,4 ± 4,8 | 9,0 |
| Земля | 3,8 | 5,0 ± 1,2 | 4,0 |
| Марс | 1,35 | 1,1 ± 0,3 | 1,4 |
| Икар | 10,1 | 9,8 ± 0,8 | 6,9 |
Выводы:
Аномальное смещение перигелия планет зависит только от орбитальной скорости. Расстояние до гравитирующего центра влияет только на изменение орбитальной скорости. Модель дает детальное описание процессов. Скорость света в формуле абсолютно неслучайна и физически обоснована. Она не относится ни к скорости гравитации (Гербер), ни к гравитационному радиусу Солнца (Эйнштейн).
Виктор Петров
P.S.
Смещение периастра PSR J0737−3039
Для проверки использовал разные методы (задача двух тел, метод встречных скоростей) и разные данные.
Разброс значений от 15,2 градуса в год до 17,5 градуса в год. Наиболее достоверными считаю данные A Review of The Double Pulsar - PSR J0737−3039. По ним получен результат 17,5 гр/год. Сами они дают 17,88 гр/год.
Меньше всего данных о расстоянии между компонентами А и В.
Ввиду малости эксцентриситета в расчет его не принимал.
И вот хочется переписать формулу, данную мною для смещения перицентров.
Вместо лучше использовать
где - угол полного оборота, а второе
- число.
В общем случае
где - любой угол перемещения положения тела на орбите.







СТО полностью ошибочна, т.к. основана на неверном виде преобразований: в них потерян масштабный множитель, характеризующий эффект Доплера. Сначала Лоренц рассматривал более общий вид преобразований (с масштабным множителем), но затем он, а также Пуанкаре и Эйнштейн приравняли его 1 без должных оснований. Их вид был искусственно сужен, формулы стали неверными, что привело к неразрешимым логическим парадоксам. Соответственно, ОТО также неверна.Из исправленных преобразований сразу следует, что потенциал Гербера правилен.Подробнее см. мою брошюру "Мемуар по теории относительности и единой теории поля" (2000).На русском: http://viXra.org/abs/1801.0305На англ.: http://vixra.org/abs/1802.0136
Есть один маленький нюанс в аномальных перигелиях. Если решить задачку о нахождении аномального ускорения вызывающего аномальный сдвиг перигелия, то значение аномального ускорения Меркурия равно 1.2122*10^-10 м/с². Бьюсь об заклад, ни кто на Земле не находил ускорение вызывающее сдвиг в 43" за сто лет. Так вот кто не в курсе это ускорение Меркурия близко к необьяснимой части аномального ускорения "Пионеров" а=2.5*10^-10м/с² и точно совпадает с аномальным ускорением звезд в рукавах спиральных галактик. Называемое ускорением Милгрома и равным а=1.2*10^-10м/с². Проблема перигелия Меркурия, не локальная проблема кучки гравитирующих тел, а проблема внегалактической природы. Кто не верит, может сам расчитать аномальное ускорение Меркурия.
aeromash@gmail.com
Движение перигелия - это свойство вещества, а значит это вообще не проблема.
Проблема не в веществе, проблема в причине его движения. Если бы это была не проблема, то нас бы здесь не было.
Причина не в движении вещества, а в его строении и способе движения.