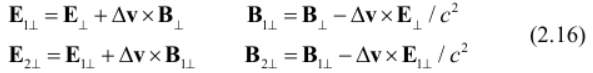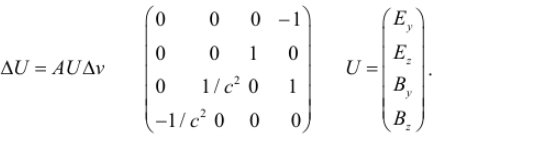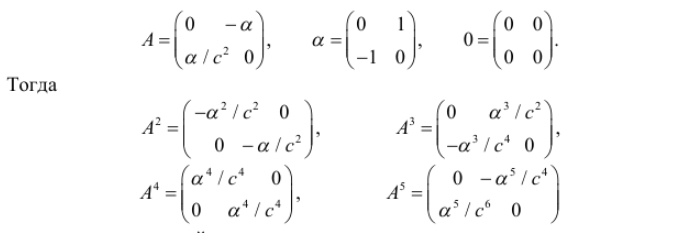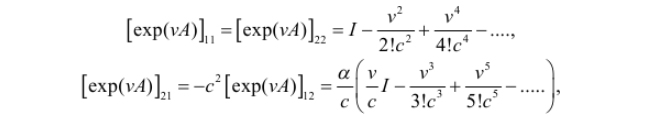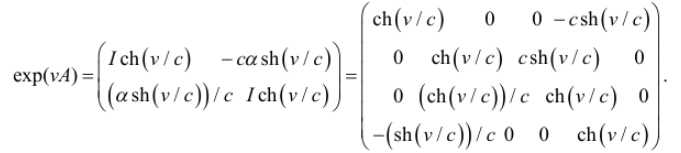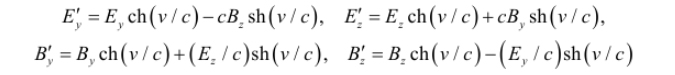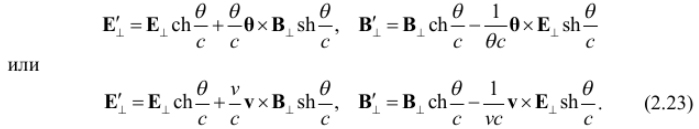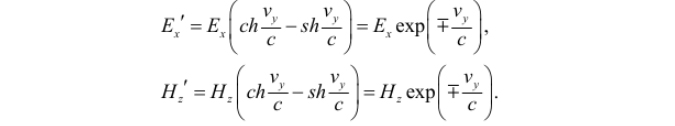–í —Å—Ç–∞—Ç—å–µ –ø–æ–ª—É—á–µ–Ω—ã –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è –ø–æ–ª–µ–π –ø—Ä–∏ –ø–µ—Ä–µ—Ö–æ–¥–µ –∏–∑ –æ–¥–Ω–æ–π –ò–°–û –≤ –¥—Ä—É–≥—É—é. –í –æ—Ç–ª–∏—á–∏–µ –æ—Ç –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏–π –õ–æ—Ä–µ–Ω—Ü–∞ –æ—Å–Ω–æ–≤–æ–π —Ç–∞–∫–∏—Ö –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏–π —è–≤–ª—è—é—Ç—Å—è –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è –ì–∞–ª–∏–ª–µ—è –∏ —Å–∏–º–º–µ—Ç—Ä–∏—á–Ω—ã–µ –∑–∞–∫–æ–Ω—ã –∏–Ω–¥—É–∫—Ü–∏–∏. –ü—Ä–∏ —ç—Ç–æ–º –∏—Å–ø–æ–ª—å–∑—É—é—Ç—Å—è –ø–æ–ª–Ω—ã–µ –ø—Ä–æ–∏–∑–≤–æ–¥–Ω—ã–µ, —É—á–∏—Ç—ã–≤–∞—é—â–∏–µ –∫–æ–Ω–≤–µ–∫—Ç–∏–≤–Ω—É—é –∏—Ö —á–∞—Å—Ç—å. –≠—Ç–æ –¥–∞–ª–æ –≤–æ–∑–º–æ–∂–Ω–æ—Å—Ç—å –æ–±—ä—è—Å–Ω–∏—Ç—å —è–≤–ª–µ–Ω–∏–µ —Ñ–∞–∑–æ–≤–æ–π –∞–±–µ—Ä—Ä–∞—Ü–∏–∏ —Å–≤–µ—Ç–∞ –∏ –≤—ã—è—Å–Ω–∏—Ç—å –ø—Ä–∏—á–∏–Ω—ã –ø–æ–ø–µ—Ä–µ—á–Ω–æ–≥–æ —ç—Ñ—Ñ–µ–∫—Ç–∞ –î–æ–ø–ª–µ—Ä–∞, –∫–æ—Ç–æ—Ä—ã–π —è–≤–ª—è–µ—Ç—Å—è —Ç–æ–ª—å–∫–æ –∫–∞–∂—É—â–∏–º—Å—è —ç—Ñ—Ñ–µ–∫—Ç–æ–º.
–ö–ª—é—á–µ–≤—ã–µ —Å–ª–æ–≤–∞: –∑–∞–∫–æ–Ω—ã –∏–Ω–¥—É–∫—Ü–∏–∏, —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–µ –ø–æ–ª–µ, –º–∞–≥–Ω–∏—Ç–Ω–æ–µ –ø–æ–ª–µ, –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è –ì–∞–ª–∏–ª–µ—è, –ü—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è –õ–æ—Ä–µ–Ω—Ü–∞, —Ñ–∞–∑–æ–≤–∞—è –∞–±–µ—Ä—Ä–∞—Ü–∏—è —Å–≤–µ—Ç–∞, –ø–æ–ø–µ—Ä–µ—á–Ω—ã–π —ç—Ñ—Ñ–µ–∫—Ç –î–æ–ø–ª–µ—Ä–∞.
1. –í–≤–µ–¥–µ–Ω–∏–µ
–°–ø–µ—Ü–∏–∞–ª—å–Ω–∞—è —Ç–µ–æ—Ä–∏—è –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ—Å—Ç–∏ (–°–¢–û) –±—ã–ª–∞ —Ä–∞–∑—Ä–∞–±–æ—Ç–∞–Ω–∞ –ê–ª—å–±–µ—Ä—Ç–æ–º –≠–π–Ω—à—Ç–µ–π–Ω–æ–º –≤ 1905 –≥. –ï—ë –æ—Å–Ω–æ–≤–æ–π —è–≤–ª—è—é—Ç—Å—è –ø–æ—Å—Ç—É–ª–∞—Ç—ã, –æ–¥–∏–Ω –∏–∑ –∫–æ—Ç–æ—Ä—ã—Ö (—Ç–∞–∫ –Ω–∞–∑—ã–≤–∞–µ–º—ã–π –≤—Ç–æ—Ä–æ–π –ø–æ—Å—Ç—É–ª–∞—Ç) –≥–ª–∞—Å–∏—Ç, —á—Ç–æ —Å–∫–æ—Ä–æ—Å—Ç—å —Å–≤–µ—Ç–∞ —è–≤–ª—è–µ—Ç—Å—è –∏–Ω–≤–∞—Ä–∏–∞–Ω—Ç–æ–º, —Ç.–µ. –Ω–µ –∑–∞–≤–∏—Å–∏—Ç –æ—Ç —Å–∏—Å—Ç–µ–º—ã –Ω–∞–±–ª—é–¥–µ–Ω–∏—è. –≠—Ç–æ –æ–∑–Ω–∞—á–∞–µ—Ç, —á—Ç–æ –Ω–∏ –ø—Ä–∏ –∫–∞–∫–∏—Ö –æ–±—Å—Ç–æ—è—Ç–µ–ª—å—Å—Ç–≤–∞—Ö —Å–∫–æ—Ä–æ—Å—Ç—å —Å–≤–µ—Ç–∞ –Ω–µ –º–æ–∂–µ—Ç –ø—Ä–µ–≤—ã—Å–∏—Ç—å –µ—ë —Å—Ç–∞–Ω–¥–∞—Ä—Ç–Ω–æ–≥–æ –∑–Ω–∞—á–µ–Ω–∏—è, –∫–æ—Ç–æ—Ä–æ–µ –≤ –≤–∞–∫—É—É–º–µ —Ä–∞–≤–Ω–æ 299¬Ý792¬Ý458 ¬± 1,2¬Ý–º/—Å (–æ–∫—Ä—É–≥–ª—ë–Ω–Ω–æ 300000 –∫–º/—Å). –í—Ç–æ—Ä–æ–π –ø–æ—Å—Ç—É–ª–∞—Ç –°–¢–û –ø—Ä–æ—Ç–∏–≤–æ—Ä–µ—á–∏—Ç –∑–¥—Ä–∞–≤–æ–º—É —Å–º—ã—Å–ª—É, –ø–æ—Å–∫–æ–ª—å–∫—É —Å–∫–æ—Ä–æ—Å—Ç—å –µ—Å—Ç—å –≤–µ–ª–∏—á–∏–Ω–∞ –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–∞—è. –ü–∞—Å—Å–∞–∂–∏—Ä, –µ–¥—É—â–∏–π –≤ –≤–∞–≥–æ–Ω–µ –ø–æ–µ–∑–¥–∞, –ø–æ –æ—Ç–Ω–æ—à–µ–Ω–∏—é –∫ –≤–∞–≥–æ–Ω—É –Ω–µ–ø–æ–¥–≤–∏–∂–µ–Ω, –ø–æ –æ—Ç–Ω–æ—à–µ–Ω–∏—é –∂–µ –∫ —Å—Ç–∞–Ω—Ü–∏–æ–Ω–Ω—ã–º –ø–æ—Å—Ç—Ä–æ–π–∫–∞–º –æ–Ω –¥–≤–∏–∂–µ—Ç—Å—è —Å–æ —Å–∫–æ—Ä–æ—Å—Ç—å—é –ø–æ–µ–∑–¥–∞. –í –°–¢–û –≤—Å—ë —ç—Ç–æ –Ω–µ —Ç–∞–∫. –ï—Å–ª–∏ –≤–Ω—É—Ç—Ä–∏ –≤–∞–≥–æ–Ω–∞ –ª—É—á —Å–≤–µ—Ç–∞ –¥–≤–∏–∂–µ—Ç—Å—è —Å–æ —Å—Ç–∞–Ω–¥–∞—Ä—Ç–Ω–æ–π —Å–∫–æ—Ä–æ—Å—Ç—å—é, —Ç–æ –∏ –ø–æ –æ—Ç–Ω–æ—à–µ–Ω–∏—é –∫ —Å—Ç–∞–Ω—Ü–∏–æ–Ω–Ω—ã–º –ø–æ—Å—Ç—Ä–æ–π–∫–∞–º –æ–Ω –¥–≤–∏–∂–µ—Ç—Å—è —Å —Ç–∞–∫–æ–π –∂–µ —Å–∫–æ—Ä–æ—Å—Ç—å—é.
–° –º–æ–º–µ–Ω—Ç–∞ —Å–æ–∑–¥–∞–Ω–∏—è –°–¢–û –±—ã–ª–∏ –ø—Ä–æ–≤–µ–¥–µ–Ω—ã –º–Ω–æ–≥–æ—á–∏—Å–ª–µ–Ω–Ω—ã–µ —ç–∫—Å–ø–µ—Ä–∏–º–µ–Ω—Ç—ã, –≤ –∫–æ—Ç–æ—Ä—ã—Ö —ç–∫—Å–ø–µ—Ä–∏–º–µ–Ω—Ç–∞—Ç–æ—Ä—ã –ø—ã—Ç–∞–ª–∏—Å—å –¥–æ–∫–∞–∑–∞—Ç—å –æ—à–∏–±–æ—á–Ω–æ—Å—Ç—å –≤—Ç–æ—Ä–æ–≥–æ –ø–æ—Å—Ç—É–ª–∞—Ç–∞. –î–ª—è —ç—Ç–æ–≥–æ –æ–Ω–∏ –∏—Å–ø–æ–ª—å–∑–æ–≤–∞–ª–∏ –∏—Å—Ç–æ—á–Ω–∏–∫–∏ –∏–∑–ª—É—á–µ–Ω–∏—è, –∫–æ—Ç–æ—Ä—ã–µ –¥–≤–∏–≥–∞–ª–∏—Å—å –ø–æ –æ—Ç–Ω–æ—à–µ–Ω–∏—é –∫ —Å–∏—Å—Ç–µ–º–µ –Ω–∞–±–ª—é–¥–µ–Ω–∏—è —Å –∑–∞–¥–∞–Ω–Ω–æ–π —Å–∫–æ—Ä–æ—Å—Ç—å—é, –Ω–æ, –ø–æ–ª—É—á–µ–Ω–Ω—ã–µ –≤ —Ç–∞–∫–∏—Ö —ç–∫—Å–ø–µ—Ä–∏–º–µ–Ω—Ç–∞—Ö –∑–Ω–∞—á–µ–Ω–∏—è —Å–∫–æ—Ä–æ—Å—Ç–∏ —Å–≤–µ—Ç–∞ –≤ —Å–∏—Å—Ç–µ–º–µ –Ω–∞–±–ª—é–¥–µ–Ω–∏—è –≤—Å–µ–≥–¥–∞ –æ–∫–∞–∑—ã–≤–∞–ª–∏—Å—å —Ä–∞–≤–Ω—ã–º–∏ —Å—Ç–∞–Ω–¥–∞—Ä—Ç–Ω–æ–º—É –∑–Ω–∞—á–µ–Ω–∏—é —Å–∫–æ—Ä–æ—Å—Ç–∏ —Å–≤–µ—Ç–∞ [1-9].
–¢–∞–∫–∏–µ —ç–∫—Å–ø–µ—Ä–∏–º–µ–Ω—Ç—ã –≤ —Ä–∞–∑–ª–∏—á–Ω—ã—Ö –≤–∞—Ä–∏–∞–Ω—Ç–∞—Ö –ø—Ä–æ–≤–æ–¥–∏–ª –∏ –≤—ã–¥–∞—é—â–∏–π—Å—è —É—á—ë–Ω—ã–π –ú–∞–π–∫–µ–ª—å—Å–æ–Ω, –ø—Ä–∏ –ø–æ–º–æ—â–∏ –∏–∑–æ–±—Ä–µ—Ç—ë–Ω–Ω–æ–≥–æ –∏–º –∏–Ω—Ç–µ—Ä—Ñ–µ—Ä–æ–º–µ—Ç—Ä–∞, –Ω–æ –∏ —ç—Ç–∏ —ç–∫—Å–ø–µ—Ä–∏–º–µ–Ω—Ç—ã —Ç–∞–∫–∂–µ –∑–∞–∫–æ–Ω—á–∏–ª–∏—Å—å –Ω–µ—É–¥–∞—á–µ–π.
–ò–Ω—Ç–µ—Ä—Ñ–µ—Ä–æ–º–µ—Ç—Ä –ú–∞–π–∫–µ–ª—å—Å–æ–Ω–∞ –±—ã–ª –∏–∑–æ–±—Ä–µ—Ç—ë–Ω –∞–º–µ—Ä–∏–∫–∞–Ω—Å–∫–∏–º —Ñ–∏–∑–∏–∫–æ–º –ê–ª—å–±–µ—Ä—Ç–æ–º –ê–±—Ä–∞—Ö–∞–º–æ–º –ú–∞–π–∫–µ–ª—å—Å–æ–Ω–æ–º –≤ –Ω–∞—á–∞–ª–µ –ø—Ä–æ—à–ª–æ–≥–æ –≤–µ–∫–∞. –ü—Ä–∏ –ø–æ–º–æ—â–∏ —ç—Ç–æ–≥–æ –∏–Ω—Ç–µ—Ä—Ñ–µ—Ä–æ–º–µ—Ç—Ä–∞ –±—ã–ª —Ä–µ—à–µ–Ω —Ä—è–¥ –≤–∞–∂–Ω—ã—Ö –Ω–∞—É—á–Ω—ã—Ö –∏ –ø—Ä–∏–∫–ª–∞–¥–Ω—ã—Ö –∑–∞–¥–∞—á, –≤ —á–∞—Å—Ç–Ω–æ—Å—Ç–∏ –±—ã–ª–∞ —Å –≤—ã—Å–æ–∫–æ–π —Ç–æ—á–Ω–æ—Å—Ç—å—é –∏–∑–º–µ—Ä–µ–Ω–∞ —Å–∫–æ—Ä–æ—Å—Ç—å —Å–≤–µ—Ç–∞. –û–¥–Ω–∞–∫–æ –≤ —ç–∫—Å–ø–µ—Ä–∏–º–µ–Ω—Ç–∞—Ö, –ø—Ä–æ–≤–µ–¥–µ–Ω–Ω—ã—Ö –ú–∞–π–∫–µ–ª—å—Å–æ–Ω–æ–º, –∫–∞—Å–∞—é—â–∏—Ö—Å—è –ø—Ä–æ–≤–µ—Ä–∫–∏ –≤—Ç–æ—Ä–æ–≥–æ –ø–æ—Å—Ç—É–ª–∞—Ç–∞ –°–¢–û, –±—ã–ª–∏ —Å—É—â–µ—Å—Ç–≤–µ–Ω–Ω—ã–µ –æ—à–∏–±–∫–∏. –≠—Ç–∏ –æ—à–∏–±–∫–∏ –æ–Ω —Å–æ–≤–µ—Ä—à–∏–ª, –∫–æ–≥–¥–∞ –ø—ã—Ç–∞–ª—Å—è –¥–æ–∫–∞–∑–∞—Ç—å, —á—Ç–æ —Å–∫–æ—Ä–æ—Å—Ç—å —ç–ª–µ–∫—Ç—Ä–æ–º–∞–≥–Ω–∏—Ç–Ω–æ–π (–≠–ú) –≤–æ–ª–Ω—ã —Å–∫–ª–∞–¥—ã–≤–∞–µ—Ç—Å—è —Å–æ —Å–∫–æ—Ä–æ—Å—Ç—å—é –µ—ë –∏—Å—Ç–æ—á–Ω–∏–∫–∞, —á—Ç–æ –ø—Ä–æ—Ç–∏–≤–æ—Ä–µ—á–∏–ª–æ –±—ã –≤—Ç–æ—Ä–æ–º—É –ø–æ—Å—Ç—É–ª–∞—Ç—É. –î–æ –∫–æ–Ω—Ü–∞ —Å–≤–æ–µ–π –∂–∏–∑–Ω–∏ –ú–∞–π–∫–µ–ª—å—Å–æ–Ω —Å—á–∏—Ç–∞–ª, —á—Ç–æ —Å—É—â–µ—Å—Ç–≤—É–µ—Ç —É–ø—Ä—É–≥–∞—è —Å—Ä–µ–¥–∞ (—ç—Ñ–∏—Ä), –≤ –∫–æ—Ç–æ—Ä–æ–π –∏ —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω—è—é—Ç—Å—è –≠–ú –≤–æ–ª–Ω—ã. –ü–æ—ç—Ç–æ–º—É —Ä–µ–∑—É–ª—å—Ç–∞—Ç—ã —ç–∫—Å–ø–µ—Ä–∏–º–µ–Ω—Ç–æ–≤, –∫–æ—Ç–æ—Ä—ã–µ –æ–Ω –ø—Ä–æ–≤—ë–ª –≤–º–µ—Å—Ç–µ —Å –ú–æ—Ä–ª–∏ [10] –ø–æ –æ–±–Ω–∞—Ä—É–∂–µ–Ω–∏—é —Ç–∞–∫–æ–π —Å—Ä–µ–¥—ã, –±—ã–ª–∏ –¥–ª—è –Ω–µ–≥–æ –±–æ–ª—å—à–æ–π –Ω–µ–æ–∂–∏–¥–∞–Ω–Ω–æ—Å—Ç—å—é, –ø–æ—Å–∫–æ–ª—å–∫—É —ç—Ñ–∏—Ä –æ–±–Ω–∞—Ä—É–∂–µ–Ω –Ω–µ –±—ã–ª. –ü—ã—Ç–∞—è—Å—å —É—Å–æ–≤–µ—Ä—à–µ–Ω—Å—Ç–≤–æ–≤–∞—Ç—å —ç–∫—Å–ø–µ—Ä–∏–º–µ–Ω—Ç, –æ–Ω –ø–æ–ø—ã—Ç–∞–ª—Å—è –≤ –∫–∞—á–µ—Å—Ç–≤–µ –∏—Å—Ç–æ—á–Ω–∏–∫–∞ –∏–∑–ª—É—á–µ–Ω–∏—è –∏—Å–ø–æ–ª—å–∑–æ–≤–∞—Ç—å —Å–≤–µ—Ç –∑–≤–µ–∑–¥—ã, –Ω–æ –∑–¥–µ—Å—å –µ–≥–æ –∂–¥–∞–ª–æ –µ—â—ë –±–æ–ª—å—à–∞—è –Ω–µ—É–¥–∞—á–∞. –ò—Å—Å–ª–µ–¥–æ–≤–∞–Ω–∏—è –ø–æ–∫–∞–∑–∞–ª–∏, —á—Ç–æ –∏–∑–º–µ—Ä–µ–Ω–Ω–∞—è —Å–∫–æ—Ä–æ—Å—Ç—å —Å–≤–µ—Ç–∞, –Ω–µ –∑–∞–≤–∏—Å–∏—Ç –æ—Ç —Å–∫–æ—Ä–æ—Å—Ç–∏ –∑–≤–µ–∑–¥—ã –∏ —Ä–∞–≤–Ω–∞ —Ä–∞–Ω–µ–µ –∏–∑–º–µ—Ä–µ–Ω–Ω–æ–º—É –∏–º –∂–µ —Å—Ç–∞–Ω–¥–∞—Ä—Ç–Ω–æ–º—É –∑–Ω–∞—á–µ–Ω–∏—é.
–í —Ä–∞–±–æ—Ç–∞—Ö [11,12] –ø–æ–∫–∞–∑–∞–Ω–æ, —á—Ç–æ –¥–ª—è –ø–æ–¥–æ–±–Ω—ã—Ö –∏—Å—Å–ª–µ–¥–æ–≤–∞–Ω–∏–π –∏–Ω—Ç–µ—Ä—Ñ–µ—Ä–æ–º–µ—Ç—Ä –ú–∞–π–∫–µ–ª—å—Å–æ–Ω–∞ –Ω–µ–ø—Ä–∏–≥–æ–¥–µ–Ω, —Å —á–µ–º –∏ –±—ã–ª–∏ —Å–≤—è–∑–∞–Ω—ã –µ–≥–æ –æ—à–∏–±–∫–∏. –ò —Ç–æ–ª—å–∫–æ –ø–æ—Å–ª–µ –∏–∑–æ–±—Ä–µ—Ç–µ–Ω–∏—è –∏–Ω—Ç–µ—Ä—Ñ–µ—Ä–æ–º–µ—Ç—Ä–∞ —Å –º–µ—Ö–∞–Ω–∏—á–µ—Å–∫–∏–º –¥–µ–ª–µ–Ω–∏–µ–º –ª—É—á–∞ —Å—Ç–∞–ª–∞ –≤–æ–∑–º–æ–∂–Ω–∞ –∫–æ—Ä—Ä–µ–∫—Ç–Ω–∞—è –ø—Ä–æ–≤–µ—Ä–∫–∞ –≤—Ç–æ—Ä–æ–≥–æ –ø–æ—Å—Ç—É–ª–∞—Ç–∞ —Ç–µ–æ—Ä–∏–∏ –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ—Å—Ç–∏ [11]. –Ý–µ–∑—É–ª—å—Ç–∞—Ç—ã —Ç–∞–∫–æ–π –ø—Ä–æ–≤–µ—Ä–∫–∏ –ø—Ä–µ–¥—Å—Ç–∞–≤–ª–µ–Ω—ã –≤ —Ä–∞–±–æ—Ç–µ [12], –∫–æ—Ç–æ—Ä—ã–µ –ø–æ–∫–∞–∑–∞–ª–∏, —á—Ç–æ —Å–∫–æ—Ä–æ—Å—Ç—å —Å–≤–µ—Ç–∞ —Å–∫–ª–∞–¥—ã–≤–∞–µ—Ç—Å—è —Å–æ —Å–∫–æ—Ä–æ—Å—Ç—å—é –∏—Å—Ç–æ—á–Ω–∏–∫–∞ –∏–∑–ª—É—á–µ–Ω–∏—è, —á—Ç–æ —Å–æ–æ—Ç–≤–µ—Ç—Å—Ç–≤—É–µ—Ç –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è–º –ì–∞–ª–∏–ª–µ—è, –∞ –Ω–µ –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è–º –õ–æ—Ä–µ–Ω—Ü–∞. –ù–æ –µ—Å–ª–∏ —ç—Ç–æ —Ç–∞–∫ –∏ –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è –õ–æ—Ä–µ–Ω—Ü–∞ –æ—à–∏–±–æ—á–Ω—ã, —Ç–æ —Å–ª–µ–¥—É–µ—Ç –∏—Å–∫–∞—Ç—å –∏–º –∑–∞–º–µ–Ω—É. –≠—Ç–æ–º—É –≤–æ–ø—Ä–æ—Å—É –∏ –ø–æ—Å–≤—è—â–µ–Ω–∞ –ø—Ä–µ–¥–ª–∞–≥–∞–µ–º–∞—è —Å—Ç–∞—Ç—å—è.
2. –ü—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è –ú–µ–Ω–¥–µ –≤ –∫–æ–Ω—Ü–µ–ø—Ü–∏–∏ —Å–∫–∞–ª—è—Ä–Ω–æ-–≤–µ–∫—Ç–æ—Ä–Ω–æ–≥–æ –ø–æ—Ç–µ–Ω—Ü–∏–∞–ª–∞
–î–ª—è —Ä–µ—à–µ–Ω–∏—è –ø–æ—Å—Ç–∞–≤–ª–µ–Ω–Ω–æ–π –∑–∞–¥–∞—á–∏ –≤—ã—è—Å–Ω–∏–º, –∫–∞–∫–∏–µ –¥–∏–Ω–∞–º–∏—á–µ—Å–∫–∏–µ –ø–æ—Ç–µ–Ω—Ü–∏–∞–ª—ã –∏ –ø–æ–ª—è –≥–µ–Ω–µ—Ä–∏—Ä—É—é—Ç –¥–≤–∏–∂—É—â–∏–µ—Å—è –∑–∞—Ä—è–¥—ã. –ü–µ—Ä–≤—ã–π —à–∞–≥ –≤ —ç—Ç–æ–º –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏–∏, –ø—Ä–æ–¥–µ–º–æ–Ω—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω–Ω—ã–π –≤ —Ä–∞–±–æ—Ç–∞—Ö [13- 15], –∫–æ–≥–¥–∞ –±—ã–ª–∏ –≤–≤–µ–¥–µ–Ω—ã —Å–∏–º–º–µ—Ç—Ä–∏—á–Ω—ã–µ –∑–∞–∫–æ–Ω—ã –º–∞–≥–Ω–∏—Ç–æ—ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–π –∏ —ç–ª–µ–∫—Ç—Ä–æ–º–∞–≥–Ω–∏—Ç–Ω–æ–π –∏–Ω–¥—É–∫—Ü–∏–∏. –û–Ω–∏ –∑–∞–ø–∏—Å—ã–≤–∞—é—Ç—Å—è –≤ —Å–ª–µ–¥—É—é—â–µ–º –≤–∏–¥–µ [16-20]:
–∏–ª–∏
–î–ª—è –ø–æ—Å—Ç–æ—è–Ω–Ω—ã—Ö –ø–æ–ª–µ–π —ç—Ç–∏ —Å–æ–æ—Ç–Ω–æ—à–µ–Ω–∏—è –∏–º–µ—é—Ç –≤–∏–¥:
–°–æ–æ—Ç–Ω–æ—à–µ–Ω–∏—è (2.3) —Å–≤–∏–¥–µ—Ç–µ–ª—å—Å—Ç–≤—É—é—Ç –æ —Ç–æ–º, —á—Ç–æ –≤ —Å–ª—É—á–∞–µ –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ–≥–æ –¥–≤–∏–∂–µ–Ω–∏—è —Å–∏—Å—Ç–µ–º –æ—Ç—Å—á–µ—Ç–∞, –º–µ–∂–¥—É –ø–æ–ª—è–º–∏¬ÝE¬Ý–∏¬ÝH¬Ý—Å—É—â–µ—Å—Ç–≤—É–µ—Ç –ø–µ—Ä–µ–∫—Ä–µ—Å—Ç–Ω–∞—è —Å–≤—è–∑—å, —Ç.–µ. –¥–≤–∏–∂–µ–Ω–∏–µ –≤ –ø–æ–ª—è—Ö¬ÝH¬Ý–ø—Ä–∏–≤–æ–¥–∏—Ç –∫ –ø–æ—è–≤–ª–µ–Ω–∏—é –ø–æ–ª–µ–π¬Ý–ï¬Ý–∏ –Ω–∞–æ–±–æ—Ä–æ—Ç.
–í —Å–æ–æ—Ç–Ω–æ—à–µ–Ω–∏—è—Ö (2.1)-(2.3), –æ—Å–Ω–æ–≤–∞–Ω–Ω—ã—Ö –Ω–∞ –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è—Ö –ì–∞–ª–∏–ª–µ—è, —à—Ç—Ä–∏—Ö–æ–≤–∞–Ω–Ω—ã–µ –∏ –Ω–µ —à—Ç—Ä–∏—Ö–æ–≤–∞–Ω–Ω—ã–µ –≤–µ–ª–∏—á–∏–Ω—ã –ø—Ä–µ–¥—Å—Ç–∞–≤–ª—è—é—Ç –ø–æ–ª—è –∏ —ç–ª–µ–º–µ–Ω—Ç—ã –≤ –¥–≤–∏–∂—É—â–µ–π—Å—è –∏ –Ω–µ–ø–æ–¥–≤–∏–∂–Ω–æ–π –ò–°–û —Å–æ–æ—Ç–≤–µ—Ç—Å—Ç–≤–µ–Ω–Ω–æ. –ó–∞–º–µ—Ç–∏–º, —á—Ç–æ –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è (2.3) —Ä–∞–Ω–µ–µ –ø–æ–ª—É—á–∞–ª–∏ —Ç–æ–ª—å–∫–æ –∏–∑ –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏–π –õ–æ—Ä–µ–Ω—Ü–∞.
Соотношения (2.1)–(2.3), представляющие законы индукции, не дают информации о возникновении полей в исходной неподвижной ИСО. Они описывают только закономерности распространения и преобразования полей в случае движения по отношению к уже существующим полям.
–°–æ–æ—Ç–Ω–æ—à–µ–Ω–∏—è (2.3) —Å–≤–∏–¥–µ—Ç–µ–ª—å—Å—Ç–≤—É—é—Ç –æ —Ç–æ–º, —á—Ç–æ –≤ —Å–ª—É—á–∞–µ –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ–≥–æ –¥–≤–∏–∂–µ–Ω–∏—è —Å–∏—Å—Ç–µ–º –æ—Ç—Å—á–µ—Ç–∞, –º–µ–∂–¥—É –ø–æ–ª—è–º–∏ E –∏ H —Å—É—â–µ—Å—Ç–≤—É–µ—Ç –ø–µ—Ä–µ–∫—Ä–µ—Å—Ç–Ω–∞—è —Å–≤—è–∑—å, —Ç.–µ. –¥–≤–∏–∂–µ–Ω–∏–µ –≤ –ø–æ–ª—è—Ö H –ø—Ä–∏–≤–æ–¥–∏—Ç –∫ –ø–æ—è–≤–ª–µ–Ω–∏—é –ø–æ–ª–µ–π r –∏ –Ω–∞–æ–±–æ—Ä–æ—Ç. –ò–∑ —ç—Ç–∏—Ö —Å–æ–æ—Ç–Ω–æ—à–µ–Ω–∏–π –≤—ã—Ç–µ–∫–∞—é—Ç –¥–æ–ø–æ–ª–Ω–∏—Ç–µ–ª—å–Ω—ã–µ —Å–ª–µ–¥—Å—Ç–≤–∏—è, –≤–ø–µ—Ä–≤—ã–µ —Ä–∞—Å—Å–º–æ—Ç—Ä–µ–Ω–Ω—ã–µ –≤ —Ä–∞–±–æ—Ç–∞—Ö [13-15,21].
–ï—Å–ª–∏ –∑–∞—Ä—è–∂–µ–Ω–Ω—ã–π —Å—Ç–µ—Ä–∂–µ–Ω—å –∏–º–µ–µ—Ç –ø–æ–≥–æ–Ω–Ω—ã–π –∑–∞—Ä—è–¥ g, —Ç–æ –µ–≥–æ —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–µ –ø–æ–ª–µ¬Ý¬Ý—É–±—ã–≤–∞–µ—Ç –ø–æ –∑–∞–∫–æ–Ω—É 1/r, –≥–¥–µ r - —Ä–∞—Å—Å—Ç–æ—è–Ω–∏–µ –æ—Ç —Ü–µ–Ω—Ç—Ä–∞–ª—å–Ω–æ–π –æ—Å–∏ —Å—Ç–µ—Ä–∂–Ω—è –¥–æ —Ç–æ—á–∫–∏ –Ω–∞–±–ª—é–¥–µ–Ω–∏—è.
–ï—Å–ª–∏ –ø–∞—Ä–∞–ª–ª–µ–ª—å–Ω–æ –æ—Å–∏ —Å—Ç–µ—Ä–∂–Ω—è –≤ –ø–æ–ª–µ E –¥–≤–∏–≥–∞—Ç—å —Å–æ —Å–∫–æ—Ä–æ—Å—Ç—å—é¬Ý –¥—Ä—É–≥—É—é –ò–°–û, —Ç–æ –≤ –Ω–µ–π –ø–æ—è–≤–∏—Ç—Å—è –¥–æ–ø–æ–ª–Ω–∏—Ç–µ–ª—å–Ω–æ–µ –º–∞–≥–Ω–∏—Ç–Ω–æ–µ –ø–æ–ª–µ
. –ï—Å–ª–∏ —Ç–µ–ø–µ—Ä—å –ø–æ –æ—Ç–Ω–æ—à–µ–Ω–∏—é –∫ —É–∂–µ –¥–≤–∏–∂—É—â–µ–π—Å—è –ò–°–û –¥–≤–∏–≥–∞—Ç—å —Ç—Ä–µ—Ç—å—é —Å–æ —Å–∫–æ—Ä–æ—Å—Ç—å—é
, —Ç–æ —É–∂–µ –∑–∞ —Å—á–µ—Ç –¥–≤–∏–∂–µ–Ω–∏—è –≤ –ø–æ–ª–µ
¬Ý–ø–æ—è–≤–∏—Ç—Å—è –¥–æ–±–∞–≤–∫–∞ –∫ —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–º—É –ø–æ–ª—é
¬Ý–∏ —Ç.–¥. –ü–æ–ª—É—á–∞–µ—Ç—Å—è —Ä—è–¥, –¥–∞—é—â–∏–π –≤–µ–ª–∏—á–∏–Ω—É —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–≥–æ –ø–æ–ª—è
¬Ý–≤ –¥–≤–∏–∂—É—â–µ–π—Å—è –ò–°–û –ø—Ä–∏ –¥–æ—Å—Ç–∏–∂–µ–Ω–∏–∏ —Å–∫–æ—Ä–æ—Å—Ç–∏
, –∫–æ–≥–¥–∞
, –∞
. –í –∫–æ–Ω–µ—á–Ω–æ–º –∏—Ç–æ–≥–µ, –≤ –¥–≤–∏–∂—É—â–µ–π—Å—è –ò–°–û –≤–µ–ª–∏—á–∏–Ω–∞ –¥–∏–Ω–∞–º–∏—á–µ—Å–∫–æ–≥–æ —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–≥–æ –ø–æ–ª—è –æ–∫–∞–∂–µ—Ç—Å—è –±–æ–ª—å—à–µ, —á–µ–º –≤ –∏—Å—Ö–æ–¥–Ω–æ–π, –∏ –∑–∞–≤–∏—Å—è—â–µ–π –æ—Ç –Ω–æ—Ä–º–∞–ª—å–Ω–æ–π —Å–æ—Å—Ç–∞–≤–ª—è—é—â–µ–π —Å–∫–æ—Ä–æ—Å—Ç–∏
¬Ý–∑–∞—Ä—è–¥–∞ –∫ –≤–µ–∫—Ç–æ—Ä—É, —Å–æ–µ–¥–∏–Ω—è—é—â–µ–º—É –¥–≤–∏–∂—É—â–∏–π—Å—è –∑–∞—Ä—è–¥ –∏ —Ç–æ—á–∫—É –Ω–∞–±–ª—é–¥–µ–Ω–∏—è:
.
–≠–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–µ –ø–æ–ª–µ –æ–¥–∏–Ω–æ—á–Ω–æ–≥–æ –∑–∞—Ä—è–¥–∞ –æ–ø—Ä–µ–¥–µ–ª—è–µ—Ç—Å—è —Å–æ–æ—Ç–Ω–æ—à–µ–Ω–∏–µ–º
.
–°–∫–∞–ª—è—Ä–Ω—ã–π –ø–æ—Ç–µ–Ω—Ü–∏–∞–ª ¬Ý–¥–≤–∏–∂—É—â–µ–≥–æ—Å—è –∑–∞—Ä—è–¥–∞ –Ω–∞–∑–æ–≤—ë–º —Å–∫–∞–ª—è—Ä–Ω–æ-–≤–µ–∫—Ç–æ—Ä–Ω—ã–º (–∑–∞–≤–∏—Å–∏—Ç –Ω–µ —Ç–æ–ª—å–∫–æ –æ—Ç –≤–µ–ª–∏—á–∏–Ω—ã –∑–∞—Ä—è–¥–∞, –Ω–æ –∏ –æ—Ç —Å–∫–æ—Ä–æ—Å—Ç–∏ –∏ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏—è –µ–≥–æ –¥–≤–∏–∂–µ–Ω–∏—è –ø–æ –æ—Ç–Ω–æ—à–µ–Ω–∏—é –∫ —Ç–æ—á–∫–µ –Ω–∞–±–ª—é–¥–µ–Ω–∏—è). –û–Ω –≤—ã—Ä–∞–∂–∞–µ—Ç—Å—è —á–µ—Ä–µ–∑ —Å–∫–∞–ª—è—Ä–Ω—ã–π –ø–æ—Ç–µ–Ω—Ü–∏–∞–ª
¬Ý–Ω–µ–ø–æ–¥–≤–∏–∂–Ω–æ–≥–æ –∑–∞—Ä—è–¥–∞ —Ä–∞–≤–µ–Ω—Å—Ç–≤–æ–º
¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý¬Ý(2.4)
–ü–æ—Ç–µ–Ω—Ü–∏–∞–ª –º–∞–∫—Å–∏–º–∞–ª–µ–Ω –∏ –Ω–æ—Ä–º–∞–ª—å–Ω–æ–º –∫ –¥–≤–∏–∂–µ–Ω–∏—é –∑–∞—Ä—è–¥–∞ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏–∏. –û–Ω –æ–ø—Ä–µ–¥–µ–ª—è–µ—Ç –¥–∞–∂–µ —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–∏–µ –ø–æ–ª—è, –∏–Ω–¥—É—Ü–∏—Ä—É–µ–º—ã–µ —É—Å–∫–æ—Ä—è–µ–º—ã–º –∑–∞—Ä—è–¥–æ–º.
–ê–Ω–∞–ª–æ–≥–∏—á–Ω–æ, –¥–ª—è —Å–ª—É—á–∞—è –¥–≤–∏–∂–µ–Ω–∏—è –∑–∞—Ä—è–¥–∞ –≤ –º–∞–≥–Ω–∏—Ç–Ω–æ–º –ø–æ–ª–µ –∏–º–µ–µ–º:
.
–≥–¥–µ ¬Ý- —Å–∫–æ—Ä–æ—Å—Ç—å, –Ω–æ—Ä–º–∞–ª—å–Ω–∞—è –∫ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏—é –º–∞–≥–Ω–∏—Ç–Ω–æ–≥–æ –ø–æ–ª—è.
Получим этот результат другим способом. Обозначим полевые переменные в неподвижной системе отсчёта без штриха, а в подвижной – со штрихом. В дифференциальной форме запишем формулы взаимной индукции электрического и магнитного полей в подвижной системе отсчёта:
–∏–ª–∏, –∏–Ω–∞—á–µ,
–≥–¥–µ (2.7) —Å–æ–æ—Ç–≤–µ—Ç—Å—Ç–≤—É–µ—Ç (2.5), –∞ (2.8) —Å–æ–æ—Ç–≤–µ—Ç—Å—Ç–≤—É–µ—Ç (2.6).
–Ý–∞–∑–¥–µ–ª–∏–≤ —É—Ä–∞–≤–Ω–µ–Ω–∏—è (2.7) –∏ (2.8) –Ω–∞ E –∏ H, –ø–æ–ª—É—á–∏–º —Å–æ–æ—Ç–≤–µ—Ç—Å—Ç–≤–µ–Ω–Ω–æ:
–ü—Ä–æ–¥–∏—Ñ—Ñ–µ—Ä–µ–Ω—Ü–∏—Ä–æ–≤–∞–≤ –æ–±–µ —á–∞—Å—Ç–∏ (2.10), –∏–º–µ–µ–º:
–ü–æ–¥—Å—Ç–∞–≤–∏–≤ (2.9) –≤ (2.11), –ø–æ–ª—É—á–∏–º:
–û–±—â–∏–º —Ä–µ—à–µ–Ω–∏–µ–º –¥–∏—Ñ—Ñ–µ—Ä–µ–Ω—Ü–∏–∞–ª—å–Ω–æ–≥–æ —É—Ä–∞–≤–Ω–µ–Ω–∏—è (2.12) —è–≤–ª—è–µ—Ç—Å—è —Ñ—É–Ω–∫—Ü–∏—è
где c – скорость света в среде, C1, C2 – произвольные постоянные.
–¢–∞–∫ –∫–∞–∫ –ø—Ä–∏ ¬Ý–¥–æ–ª–∂–Ω–æ –±—ã—Ç—å –≤—ã–ø–æ–ª–Ω–µ–Ω–æ E'=E, —Ç–æ –∏–∑ (2.13) –ø–æ–ª—É—á–∏–º:
C2=1.¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý (2.14)
–ü–æ–¥—Å—Ç–∞–≤–∏–≤ (2.14) –≤ (2.13), –æ–∫–æ–Ω—á–∞—Ç–µ–ª—å–Ω–æ –∏–º–µ–µ–º –æ–±—â–µ–µ —Ä–µ—à–µ–Ω–∏–µ, –≤ –∫–æ—Ç–æ—Ä–æ–µ –≤—Ö–æ–¥–∏—Ç –æ–¥–Ω–∞ –ø—Ä–æ–∏–∑–≤–æ–ª—å–Ω–∞—è –ø–æ—Å—Ç–æ—è–Ω–Ω–∞—è C1:¬Ý
¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý
–í—ã–±–∏—Ä–∞—è C1=0, –ø–æ–ª—É—á–∞–µ–º
–ü—Ä–∏–º–µ–Ω–∏—Ç–µ–ª—å–Ω–æ –∫ —ç–ª–µ–∫—Ç—Ä–æ–º–∞–≥–Ω–∏—Ç–Ω–æ–π –≤–æ–ª–Ω–µ, –≤–≤–æ–¥—è –ø–∞—Ä–∞–ª–ª–µ–ª—å–Ω—ã–µ E‚Üë, H‚Üë¬Ý–∏ –Ω–æ—Ä–º–∞–ª—å–Ω—ã–µ ,
¬Ý—Å–∫–æ—Ä–æ—Å—Ç–∏ –ò–°–û –∫–æ–º–ø–æ–Ω–µ–Ω—Ç—ã –ø–æ–ª–µ–π, –∏–º–µ–µ–º [9]:
–≥–¥–µ ‚Äì ¬Ý- –∏–º–ø–µ–¥–∞–Ω—Å —Å–≤–æ–±–æ–¥–Ω–æ–≥–æ –ø—Ä–æ—Å—Ç—Ä–∞–Ω—Å—Ç–≤–∞,
– скорость света.
–ù–∞–∑–æ–≤—ë–º –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è –ø–æ–ª–µ–π (2.2) –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è–º–∏ –ú–µ–Ω–¥–µ.
–í—ã–≤–µ–¥–µ–º –∏—Ö –≤ –º–∞—Ç—Ä–∏—á–Ω–æ–π —Ñ–æ—Ä–º–µ [22, 23] –∏ –ø–æ–∫–∞–∂–µ–º, —á—Ç–æ –≤–∏–¥ –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏–π –æ–ø—Ä–µ–¥–µ–ª—è–µ—Ç—Å—è –∑–∞–∫–æ–Ω–æ–º —Å–ª–æ–∂–µ–Ω–∏—è —Å–∫–æ—Ä–æ—Å—Ç–µ–π (–∫–ª–∞—Å—Å–∏—á–µ—Å–∫–∏–π –∏–ª–∏ —Ä–µ–ª—è—Ç–∏–≤–∏—Å—Ç—Å–∫–∏–π).
–Ý–∞—Å—Å–º–æ—Ç—Ä–∏–º —Å–æ–≤–æ–∫—É–ø–Ω–æ—Å—Ç—å –ò–°–û —Ç–∞–∫–∏—Ö, —á—Ç–æ –ò–°–û –ö1 –¥–≤–∏–∂–µ—Ç—Å—è —Å–æ —Å–∫–æ—Ä–æ—Å—Ç—å—é –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ –ò–°–û –ö, –ò–°–û –ö2 –¥–≤–∏–∂–µ—Ç—Å—è —Å —Ç–∞–∫–æ–π –∂–µ —Å–∫–æ—Ä–æ—Å—Ç—å—é –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ –ö1 –∏ —Ç.–¥. –ï—Å–ª–∏ –º–æ–¥—É–ª—å —Å–∫–æ—Ä–æ—Å—Ç–∏ –º–∞–ª (–ø–æ —Å—Ä–∞–≤–Ω–µ–Ω–∏—é —Å–æ —Å–∫–æ—Ä–æ—Å—Ç—å—é —Å–≤–µ—Ç–∞ —Å), —Ç–æ –¥–ª—è –ø–æ–ø–µ—Ä–µ—á–Ω—ã—Ö —Å–æ—Å—Ç–∞–≤–ª—è—é—â–∏—Ö –ø–æ–ª–µ–π –≤ –ò–°–û –ö1 –ö2, –∏–º–µ–µ–º:
–∏ —Ç. –¥. –ü—Ä–∏ –ø–µ—Ä–µ—Ö–æ–¥–µ –∫ –∫–∞–∂–¥–æ–π —Å–ª–µ–¥—É—é—â–µ–π –ò–°–û –ø–æ–ª—è –ø–æ–ª—É—á–∞—é—Ç –ø—Ä–∏—Ä–∞—â–µ–Ω–∏—è –∏
:
–≥–¥–µ –ø–æ–ª—è ¬Ý–∏
¬Ý–æ—Ç–Ω–æ—Å—è—Ç—Å—è –∫ —Ç–µ–∫—É—â–µ–π –ò–°–û. –ù–∞–ø—Ä–∞–≤–ª—è—è –¥–µ–∫–∞—Ä—Ç–æ–≤—É –æ—Å—å x¬Ý–≤–¥–æ–ª—å
, –ø–µ—Ä–µ–ø–∏—à–µ–º (2.17) –≤ –∫–æ–º–ø–æ–Ω–µ–Ω—Ç–∞—Ö –≤–µ–∫—Ç–æ—Ä–∞
–°–æ–æ—Ç–Ω–æ—à–µ–Ω–∏–µ (2.18) –º–æ–∂–Ω–æ –ø—Ä–µ–¥—Å—Ç–∞–≤–∏—Ç—å –≤ –º–∞—Ç—Ä–∏—á–Ω–æ–π —Ñ–æ—Ä–º–µ
–ï—Å–ª–∏ –ø—Ä–µ–¥–ø–æ–ª–æ–∂–∏—Ç—å, —á—Ç–æ —Å–∫–æ—Ä–æ—Å—Ç—å —Å–∏—Å—Ç–µ–º—ã —Å—É–º–º–∏—Ä—É–µ—Ç—Å—è –ø–æ –∫–ª–∞—Å—Å–∏—á–µ—Å–∫–æ–º—É –∑–∞–∫–æ–Ω—É —Å–ª–æ–∂–µ–Ω–∏—è —Å–∫–æ—Ä–æ—Å—Ç–µ–π, —Ç.–µ. —Å–∫–æ—Ä–æ—Å—Ç—å –∫–æ–Ω–µ—á–Ω–æ–π –ò–°–û K'=KN¬Ý–æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ –∏—Å—Ö–æ–¥–Ω–æ–π –µ—Å—Ç—å , —Ç–æ –ø–æ–ª—É—á–∏–º –º–∞—Ç—Ä–∏—á–Ω—É—é —Å–∏—Å—Ç–µ–º—É –¥–∏—Ñ—Ñ–µ—Ä–µ–Ω—Ü–∏–∞–ª—å–Ω—ã—Ö —É—Ä–∞–≤–Ω–µ–Ω–∏–π
¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý (2.19)
—Å –Ω–µ–∑–∞–≤–∏—Å—è—â–µ–π –æ—Ç —Å–∫–æ—Ä–æ—Å—Ç–∏ –º–∞—Ç—Ä–∏—Ü–µ–π —Å–∏—Å—Ç–µ–º—ã
. –Ý–µ—à–µ–Ω–∏–µ —Å–∏—Å—Ç–µ–º—ã –≤—ã—Ä–∞–∂–∞–µ—Ç—Å—è —á–µ—Ä–µ–∑ –º–∞—Ç—Ä–∏—á–Ω—É—é —ç–∫—Å–ø–æ–Ω–µ–Ω—Ç—É exp(vA):
¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý (2.20)
–ó–¥–µ—Å—å - –º–∞—Ç—Ä–∏—Ü–∞-—Å—Ç–æ–ª–±–µ—Ü –ø–æ–ª–µ–π –≤ —Å–∏—Å—Ç–µ–º–µ
, –∞
- –º–∞—Ç—Ä–∏—Ü–∞-—Å—Ç–æ–ª–±–µ—Ü –ø–æ–ª–µ–π –≤ —Å–∏—Å—Ç–µ–º–µ
. –ü–æ–¥—Å—Ç–∞–≤–ª—è—è (2.20) –≤ —Å–∏—Å—Ç–µ–º—É (2.19), —É–±–µ–∂–¥–∞–µ–º—Å—è, —á—Ç–æ
–¥–µ–π—Å—Ç–≤–∏—Ç–µ–ª—å–Ω–æ —è–≤–ª—è–µ—Ç—Å—è —Ä–µ—à–µ–Ω–∏–µ–º —Å–∏—Å—Ç–µ–º—ã (2.19):
–û—Å—Ç–∞—ë—Ç—Å—è –Ω–∞–π—Ç–∏ —ç—Ç—É —ç–∫—Å–ø–æ–Ω–µ–Ω—Ç—É —Ä–∞–∑–ª–æ–∂–µ–Ω–∏–µ–º –µ—ë –≤ —Ä—è–¥:
–≥–¥–µ - –µ–¥–∏–Ω–∏—á–Ω–∞—è –º–∞—Ç—Ä–∏—Ü–∞ —Ä–∞–∑–º–µ—Ä–æ–º 4 x 4. –î–ª—è —ç—Ç–æ–≥–æ —É–¥–æ–±–Ω–æ –∑–∞–ø–∏—Å–∞—Ç—å
–º–∞—Ç—Ä–∏—Ü—É –≤ –±–ª–æ—á–Ω–æ–π —Ñ–æ—Ä–º–µ
–∏ —ç–ª–µ–º–µ–Ω—Ç—ã –º–∞—Ç—Ä–∏—á–Ω–æ–π —ç–∫—Å–ø–æ–Ω–µ–Ω—Ç—ã –∏–º–µ—é—Ç –≤–∏–¥
–≥–¥–µ ¬Ý- –µ–¥–∏–Ω–∏—á–Ω–∞—è –º–∞—Ç—Ä–∏—Ü–∞ 2 x 2. –ù–µ—Ç—Ä—É–¥–Ω–æ –≤–∏–¥–µ—Ç—å, —á—Ç–æ
, –ø–æ—ç—Ç–æ–º—É –æ–∫–æ–Ω—á–∞—Ç–µ–ª—å–Ω–æ –ø–æ–ª—É—á–∞–µ–º
–¢–µ–ø–µ—Ä—å –≤–æ–∑–≤—Ä–∞—â–∞–µ–º—Å—è –∫ (2.20) –∏ –ø–æ–¥—Å—Ç–∞–≤–ª—è—è —Ç—É–¥–∞ , –Ω–∞—Ö–æ–¥–∏–º
–∏–ª–∏ –≤ –≤–µ–∫—Ç–æ—Ä–Ω–æ–π –∑–∞–ø–∏—Å–∏
–≠—Ç–æ –∏ –µ—Å—Ç—å –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è (2.2).
–í–æ–∑–Ω–∏–∫–∞–µ—Ç –∑–∞–∫–æ–Ω–æ–º–µ—Ä–Ω—ã–π –≤–æ–ø—Ä–æ—Å, –ø–æ—á–µ–º—É –æ–Ω–∏ –æ—Ç–ª–∏—á–∞—é—Ç—Å—è –æ—Ç —Å–æ–æ—Ç–≤–µ—Ç—Å—Ç–≤—É—é—â–∏—Ö –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏–π –ø–æ–ª–µ–π –≤ –°–¢–û, –≤–µ–¥—å –≤ –Ω–µ–π –ø—Ä–∏ –º–∞–ª—ã—Ö —Å–∫–æ—Ä–æ—Å—Ç—è—Ö –∏–º–µ—é—Ç –º–µ—Å—Ç–æ –∏—Å—Ö–æ–¥–Ω—ã–µ —Å–æ–æ—Ç–Ω–æ—à–µ–Ω–∏—è (2.16) –∏ (2.17). –î–µ–ª–æ –≤ —Ç–æ–º, —á—Ç–æ —Å–æ–≥–ª–∞—Å–Ω–æ —Ä–µ–ª—è—Ç–∏–≤–∏—Å—Ç—Å–∫–æ–º—É –∑–∞–∫–æ–Ω—É —Å–ª–æ–∂–µ–Ω–∏—è —Å–∫–æ—Ä–æ—Å—Ç–µ–π —Å–∫–ª–∞–¥—ã–≤–∞—é—Ç—Å—è –Ω–µ —Å–∫–æ—Ä–æ—Å—Ç–∏ –ò–°–û, –∞ –∏—Ö –±—ã—Å—Ç—Ä–æ—Ç—ã (https://ru.wikipedia.org/wiki/ –ë—ã—Å—Ç—Ä–æ—Ç–∞). –°–æ–≥–ª–∞—Å–Ω–æ –æ–ø—Ä–µ–¥–µ–ª–µ–Ω–∏—é, –±—ã—Å—Ç—Ä–æ—Ç–∞ –≤–≤–æ–¥–∏—Ç—Å—è –∫–∞–∫
¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý(2.22)
–ò–º–µ–Ω–Ω–æ, –µ—Å–ª–∏ –±—ã—Å—Ç—Ä–æ—Ç—ã —Å–∏—Å—Ç–µ–º K1¬Ý–∏ K, K2¬Ý–∏ K1, K3¬Ý–∏ K2¬Ý–∏ —Ç.–¥. –æ—Ç–ª–∏—á–∞—é—Ç—Å—è –Ω–∞ , —Ç–æ –±—ã—Å—Ç—Ä–æ—Ç–∞ –ò–°–û K'=KN¬Ý–æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω–æ K¬Ý–µ—Å—Ç—å
. –ü—Ä–∏ –º–∞–ª—ã—Ö —Å–∫–æ—Ä–æ—Å—Ç—è—Ö
. –ü–æ—ç—Ç–æ–º—É (2.17) –º–æ–∂–Ω–æ –∑–∞–ø–∏—Å–∞—Ç—å —Ç–∞–∫:
–≥–¥–µ v/v. –°–∏—Å—Ç–µ–º–∞ (2.19) —Å —É—á—ë—Ç–æ–º –∞–¥–¥–∏—Ç–∏–≤–Ω–æ—Å—Ç–∏ –±—ã—Å—Ç—Ä–æ—Ç—ã, –∞ –Ω–µ —Å–∫–æ—Ä–æ—Å—Ç–∏, –∑–∞–º–µ–Ω–∏—Ç—Å—è —Å–∏—Å—Ç–µ–º–æ–π —É—Ä–∞–≤–Ω–µ–Ω–∏–π
¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý¬Ý
–¢–∞–∫–∏–º –æ–±—Ä–∞–∑–æ–º, –≤—Å–µ –≤—ã–∫–ª–∞–¥–∫–∏ –±—É–¥—É—Ç –∞–Ω–∞–ª–æ–≥–∏—á–Ω—ã –ø—Ä–∏–≤–µ–¥–µ–Ω–Ω—ã–º –≤—ã—à–µ —Å —Ç–æ–π —Ä–∞–∑–Ω–∏—Ü–µ–π, —á—Ç–æ –≤–º–µ—Å—Ç–æ —Å–∫–æ—Ä–æ—Å—Ç–µ–π –≤ –≤—ã—Ä–∞–∂–µ–Ω–∏—è—Ö –±—É–¥–µ—Ç —Ñ–∏–≥—É—Ä–∏—Ä–æ–≤–∞—Ç—å –±—ã—Å—Ç—Ä–æ—Ç–∞. –í —á–∞—Å—Ç–Ω–æ—Å—Ç–∏, —Ñ–æ—Ä–º—É–ª—ã (2.21) –ø—Ä–∏–Ω–∏–º–∞—é—Ç –≤–∏–¥
–¢–∞–∫ –∫–∞–∫
—Ç–æ –ø–æ–¥—Å—Ç–∞–Ω–æ–≤–∫–∞ (2.22) –≤ (2.23) –ø—Ä–∏–≤–æ–¥–∏—Ç –∫ —Ö–æ—Ä–æ—à–æ –∏–∑–≤–µ—Å—Ç–Ω—ã–º —Ä–µ–ª—è—Ç–∏–≤–∏—Å—Ç—Å–∫–∏–º –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è–º –ø–æ–ª–µ–π
–ü—Ä–∏ –º–∞–ª—ã—Ö –æ—Ç–Ω–æ—Å–∏—Ç–µ–ª—å–Ω—ã—Ö —Å–∫–æ—Ä–æ—Å—Ç—è—Ö –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è (2.21) –∏ (2.24) —Ä–∞–∑–ª–∏—á–∞—é—Ç—Å—è, –Ω–∞—á–∏–Ω–∞—è —Å —á–ª–µ–Ω–æ–≤ —Ä–∞–∑–ª–æ–∂–µ–Ω–∏—è –ø–æ—Ä—è–¥–∫–∞ v2/c2.
–ü–æ–∫–∞–∂–µ–º, –∫–∞–∫ –ø—Ä–∏ –ø–æ–º–æ—â–∏ —Å–æ–æ—Ç–Ω–æ—à–µ–Ω–∏–π (2.2) –æ–±—ä—è—Å–Ω—è–µ—Ç—Å—è —è–≤–ª–µ–Ω–∏–µ —Ñ–∞–∑–æ–≤–æ–π –∞–±–µ—Ä—Ä–∞—Ü–∏–∏, –Ω–µ –∏–º–µ—é—â–µ–µ –æ–±—ä—è—Å–Ω–µ–Ω–∏–π –≤ —Ä–∞–º–∫–∞—Ö –∫–ª–∞—Å—Å–∏—á–µ—Å–∫–æ–π –Ω–µ—Ä–µ–ª—è—Ç–∏–≤–∏—Å—Ç—Å–∫–æ–π —ç–ª–µ–∫—Ç—Ä–æ–¥–∏–Ω–∞–º–∏–∫–∏. –ü—É—Å—Ç—å –∏–º–µ—é—Ç—Å—è –∫–æ–º–ø–æ–Ω–µ–Ω—Ç—ã –ø–ª–æ—Å–∫–æ–π –≤–æ–ª–Ω—ã Hz¬Ý–∏ Ex, —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω—è—é—â–µ–π—Å—è –≤ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏–∏ y, –∞ —à—Ç—Ä–∏—Ö–æ–≤–∞–Ω–Ω–∞—è —Å–∏—Å—Ç–µ–º–∞ –¥–≤–∏–∂–µ—Ç—Å—è –≤ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏–∏ x¬Ý—Å–æ —Å–∫–æ—Ä–æ—Å—Ç—å—é vx. –¢–æ–≥–¥–∞ –ø–æ–ª—É—á–∏–º –∫–æ–º–ø–æ–Ω–µ–Ω—Ç—ã –ø–æ–ª–µ–π –≤ —à—Ç—Ä–∏—Ö–æ–≤–∞–Ω–Ω–æ–π —Å–∏—Å—Ç–µ–º–µ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç –≤ —Å–æ–æ—Ç–≤–µ—Ç—Å—Ç–≤–∏–∏ —Å (2.2):
–¢–∞–∫–∏–º –æ–±—Ä–∞–∑–æ–º, –∏–º–µ–µ—Ç—Å—è –Ω–µ–æ–¥–Ω–æ—Ä–æ–¥–Ω–∞—è –≤–æ–ª–Ω–∞, –∏–º–µ—é—â–∞—è –≤ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏–∏ —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω–µ–Ω–∏—è –∫–æ–º–ø–æ–Ω–µ–Ω—Ç—É E'v.
–ó–∞–ø–∏—à–µ–º —Å—É–º–º–∞—Ä–Ω–æ–µ –ø–æ–ª–µ E'¬Ý–≤ –¥–≤–∏–∂—É—â–µ–π—Å—è –ò–°–û:
¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý(2.25)
–ï—Å–ª–∏ –≤–µ–∫—Ç–æ—Ä H'¬Ý–ø–æ-–ø—Ä–µ–∂–Ω–µ–º—É –æ—Ä—Ç–æ–≥–æ–Ω–∞–ª–µ–Ω –æ—Å–∏ y, —Ç–æ –≤–µ–∫—Ç–æ—Ä E'¬Ý—Ç–µ–ø–µ—Ä—å –Ω–∞–∫–ª–æ–Ω–µ–Ω –∫ –Ω–µ–π –Ω–∞ —É–≥–æ–ª , –æ–ø—Ä–µ–¥–µ–ª—è–µ–º—ã–π —Å–æ–æ—Ç–Ω–æ—à–µ–Ω–∏–µ–º:
¬Ý ¬Ý ¬Ý ¬Ý ¬Ý¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý (2.26)
–≠—Ç–æ –∏ –µ—Å—Ç—å —Ñ–∞–∑–æ–≤–∞—è –∞–±–µ—Ä—Ä–∞—Ü–∏—è —Å–≤–µ—Ç–∞. –ò–º–µ–Ω–Ω–æ –Ω–∞ —Ç–∞–∫–æ–π —É–≥–æ–ª –ø—Ä–∏—Ö–æ–¥–∏—Ç—Å—è –Ω–∞–∫–ª–æ–Ω—è—Ç—å —Ç–µ–ª–µ—Å–∫–æ–ø –ø–æ —Ö–æ–¥—É –¥–≤–∏–∂–µ–Ω–∏—è –ó–µ–º–ª–∏ –≤–æ–∫—Ä—É–≥ –°–æ–ª–Ω—Ü–∞, —á—Ç–æ–±—ã –Ω–∞–±–ª—é–¥–∞—Ç—å –∑–≤–µ–∑–¥—ã, –Ω–∞—Ö–æ–¥—è—â–∏–µ—Å—è –≤ –¥–µ–π—Å—Ç–≤–∏—Ç–µ–ª—å–Ω–æ—Å—Ç–∏ –≤ –∑–µ–Ω–∏—Ç–µ.
–í–µ–∫—Ç–æ—Ä –ü–æ–π–Ω—Ç–∏–Ω–≥a —Ç–µ–ø–µ—Ä—å —Ç–∞–∫–∂–µ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω —É–∂–µ –Ω–µ –ø–æ –æ—Å–∏ y, –∞, –Ω–∞—Ö–æ–¥—è—Å—å –≤ –ø–ª–æ—Å–∫–æ—Å—Ç–∏ xy, –Ω–∞–∫–ª–æ–Ω–µ–Ω –∫ –æ—Å–∏ y¬Ý–Ω–∞ —É–≥–æ–ª, –æ–ø—Ä–µ–¥–µ–ª—è–µ–º—ã–π (2.26). –û—Ç–Ω–æ—à–µ–Ω–∏–µ –∞–±—Å–æ–ª—é—Ç–Ω—ã—Ö –≤–µ–ª–∏—á–∏–Ω –≤–µ–∫—Ç–æ—Ä–æ–≤ E'¬Ý–∏ H'¬Ý–≤ –æ–±–µ–∏—Ö —Å–∏—Å—Ç–µ–º–∞—Ö –æ—Å—Ç–∞–ª–∏—Å—å –æ–¥–∏–Ω–∞–∫–æ–≤—ã–º–∏. –ù–æ –∞–±—Å–æ–ª—é—Ç–Ω–∞—è –≤–µ–ª–∏—á–∏–Ω–∞ –≤–µ–∫—Ç–æ—Ä–∞ –ü–æ–π–Ω—Ç–∏–Ω–≥–∞ —É–≤–µ–ª–∏—á–∏–ª–∞—Å—å. –î–∞–∂–µ –ø–æ–ø–µ—Ä–µ—á–Ω–æ–µ –∫ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏—é —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω–µ–Ω–∏—è –≤–æ–ª–Ω—ã –¥–≤–∏–∂–µ–Ω–∏–µ –ò–°–û —É–≤–µ–ª–∏—á–∏–≤–∞–µ—Ç –µ–µ —ç–Ω–µ—Ä–≥–∏—é –≤ —ç—Ç–æ–π –ò–°–û. –§–∏–∑–∏—á–µ—Å–∫–∏–π —Å–º—ã—Å–ª —è–≤–ª–µ–Ω–∏—è –ø–æ—è—Å–Ω–∏–º —Å–ª–µ–¥—É—é—â–µ–π –∞–Ω–∞–ª–æ–≥–∏–µ–π. –ö–æ–≥–¥–∞ –¥–æ–∂–¥–µ–≤—ã–µ –∫–∞–ø–ª–∏ –ø–∞–¥–∞—é—Ç –≤–µ—Ä—Ç–∏–∫–∞–ª—å–Ω–æ, —Ç–æ —ç–Ω–µ—Ä–≥–∏—è —É –Ω–∏—Ö –æ–¥–Ω–∞. –ù–æ –≤ –∏–Ω–µ—Ä—Ü–∏–∞–ª—å–Ω–æ–π —Å–∏—Å—Ç–µ–º–µ, –¥–≤–∏–≥–∞—é—â–µ–π—Å—è –Ω–æ—Ä–º–∞–ª—å–Ω–æ –∫ –≤–µ–∫—Ç–æ—Ä—É –∏—Ö —Å–∫–æ—Ä–æ—Å—Ç–∏, –∫ —ç—Ç–æ–π —Å–∫–æ—Ä–æ—Å—Ç–∏ –¥–æ–±–∞–≤–ª—è–µ—Ç—Å—è –≤–µ–∫—Ç–æ—Ä —Å–∫–æ—Ä–æ—Å—Ç–∏ –∏–Ω–µ—Ä—Ü–∏–∞–ª—å–Ω–æ–π —Å–∏—Å—Ç–µ–º—ã. –ü—Ä–∏ —ç—Ç–æ–º –∞–±—Å–æ–ª—é—Ç–Ω–∞—è –≤–µ–ª–∏—á–∏–Ω–∞ —Å–∫–æ—Ä–æ—Å—Ç–∏ –∫–∞–ø–µ–ª—å –≤ –∏–Ω–µ—Ä—Ü–∏–∞–ª—å–Ω–æ–π —Å–∏—Å—Ç–µ–º–µ –±—É–¥–µ—Ç —Ä–∞–≤–Ω–∞ –∫–æ—Ä–Ω—é –∫–≤–∞–¥—Ä–∞—Ç–Ω–æ–º—É –∏–∑ —Å—É–º–º—ã –∫–≤–∞–¥—Ä–∞—Ç–æ–≤ —É–∫–∞–∑–∞–Ω–Ω—ã—Ö —Å–∫–æ—Ä–æ—Å—Ç–µ–π. –¢–∞–∫–æ–π –∂–µ —Ä–µ–∑—É–ª—å—Ç–∞—Ç –¥–∞–µ—Ç –Ω–∞–º –∏ —Å–æ–æ—Ç–Ω–æ—à–µ–Ω–∏–µ (2.25).
–ï—Å–ª–∏ –ø–æ–ª—è—Ä–∏–∑–∞—Ü–∏—è –≤–æ–ª–Ω—ã –∏–∑–º–µ–Ω–∏—Ç—Å—è, —Ç–æ —Ä–µ–∑—É–ª—å—Ç–∞—Ç –æ—Å—Ç–∞–Ω–µ—Ç—Å—è –ø—Ä–µ–∂–Ω–∏–º, —Ç–∞–∫ –∫–∞–∫ –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è –ø–æ –æ—Ç–Ω–æ—à–µ–Ω–∏—é –∫ –≤–µ–∫—Ç–æ—Ä–∞–º E¬Ý–∏ H¬Ý–ø–æ–ª–Ω–æ—Å—Ç—å—é —Å–∏–º–º–µ—Ç—Ä–∏—á–Ω—ã. –ï–¥–∏–Ω—Å—Ç–≤–µ–Ω–Ω—ã–º –æ—Ç–ª–∏—á–∏–µ–º –±—É–¥–µ—Ç —Ç–æ, —á—Ç–æ —Ç–µ–ø–µ—Ä—å –ø–æ–ª—É—á–∏—Ç—Å—è –≤–æ–ª–Ω–∞, —É –∫–æ—Ç–æ—Ä–æ–π –ø–æ—è–≤–∏—Ç—Å—è –≤ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏–∏ —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω–µ–Ω–∏—è –∫–æ–º–ø–æ–Ω–µ–Ω—Ç–∞ H'v.
–ü–æ–ª—É—á–µ–Ω–Ω—ã–µ –≤–æ–ª–Ω—ã –∏–º–µ—é—Ç –≤ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏–∏ —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω–µ–Ω–∏—è –¥–æ–ø–æ–ª–Ω–∏—Ç–µ–ª—å–Ω—ã–µ –≤–µ–∫—Ç–æ—Ä–∞ —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–≥–æ –∏–ª–∏ –º–∞–≥–Ω–∏—Ç–Ω–æ–≥–æ –ø–æ–ª—è, –∏ –≤ —ç—Ç–æ–º –æ–Ω–∏ –ø–æ—Ö–æ–∂–∏ –Ω–∞ E¬Ý–∏ H¬Ý–≤–æ–ª–Ω—ã, —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω—è—é—â–∏–µ—Å—è –≤ –≤–æ–ª–Ω–æ–≤–æ–¥–∞—Ö. –í –¥–∞–Ω–Ω–æ–º —Å–ª—É—á–∞–µ –≤–æ–∑–Ω–∏–∫–∞–µ—Ç –Ω–µ–æ–±—ã—á–Ω–∞—è –≤–æ–ª–Ω–∞, —É –∫–æ—Ç–æ—Ä–æ–π —Ñ–∞–∑–æ–≤—ã–π —Ñ—Ä–æ–Ω—Ç –Ω–∞–∫–ª–æ–Ω–µ–Ω –∫ –≤–µ–∫—Ç–æ—Ä—É –ü–æ–π–Ω—Ç–∏–Ω–≥–∞ –Ω–∞ —É–≥–æ–ª, –æ–ø—Ä–µ–¥–µ–ª—è–µ–º—ã–π —Å–æ–æ—Ç–Ω–æ—à–µ–Ω–∏–µ–º (2.26). –ü–æ —Å—É—Ç–∏ –¥–µ–ª–∞, –ø–æ–ª—É—á–µ–Ω–Ω–∞—è –≤–æ–ª–Ω–∞ —è–≤–ª—è–µ—Ç—Å—è —Å—É–ø–µ—Ä–ø–æ–∑–∏—Ü–∏–µ–π –ø–ª–æ—Å–∫–æ–π –≤–æ–ª–Ω—ã —Å —Ñ–∞–∑–æ–≤–æ–π —Å–∫–æ—Ä–æ—Å—Ç—å—é –∏ –¥–æ–ø–æ–ª–Ω–∏—Ç–µ–ª—å–Ω–æ–π –≤–æ–ª–Ω—ã, –æ—Ä—Ç–æ–≥–æ–Ω–∞–ª—å–Ω–æ–π –∫ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏—é —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω–µ–Ω–∏—è –ø–ª–æ—Å–∫–æ–π –≤–æ–ª–Ω—ã –∏ –∏–º–µ—é—â–µ–π –±–µ—Å–∫–æ–Ω–µ—á–Ω—É—é —Ñ–∞–∑–æ–≤—É—é —Å–∫–æ—Ä–æ—Å—Ç—å.
–Ý–∞—Å—Å–º–æ—Ç—Ä–∏–º –µ—â–µ –æ–¥–∏–Ω —Å–ª—É—á–∞–π, –∫–æ–≥–¥–∞ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏–µ —Å–∫–æ—Ä–æ—Å—Ç–∏ –¥–≤–∏–∂—É—â–µ–π—Å—è —Å–∏—Å—Ç–µ–º—ã —Å–æ–≤–ø–∞–¥–∞–µ—Ç —Å –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏–µ–º —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω–µ–Ω–∏—è —ç–ª–µ–∫—Ç—Ä–æ–º–∞–≥–Ω–∏—Ç–Ω–æ–π –≤–æ–ª–Ω—ã. –ë—É–¥–µ–º —Å—á–∏—Ç–∞—Ç—å, —á—Ç–æ –∏–º–µ—é—Ç—Å—è –∫–æ–º–ø–æ–Ω–µ–Ω—Ç—ã –ø–ª–æ—Å–∫–æ–π –≤–æ–ª–Ω—ã Ex¬Ý–∏ Hz, –∞ —Ç–∞–∫–∂–µ –∫–æ–º–ø–æ–Ω–µ–Ω—Ç—ã —Å–∫–æ—Ä–æ—Å—Ç–∏ . –£—á–∏—Ç—ã–≤–∞—è, —á—Ç–æ –≤ —ç—Ç–æ–º —Å–ª—É—á–∞–µ –≤—ã–ø–æ–ª–Ω—è–µ—Ç—Å—è —Å–æ–æ—Ç–Ω–æ—à–µ–Ω–∏–µ
, –ø–æ–ª—É—á–∞–µ–º, —á—Ç–æ –∞–º–ø–ª–∏—Ç—É–¥—ã –ø–æ–ª–µ–π —ç–∫—Å–ø–æ–Ω–µ–Ω—Ü–∏–∞–ª—å–Ω–æ —É–±—ã–≤–∞—é—Ç –∏–ª–∏ –≤–æ–∑—Ä–∞—Å—Ç–∞—é—Ç –≤ –∑–∞–≤–∏—Å–∏–º–æ—Å—Ç–∏ –æ—Ç –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏—è –¥–≤–∏–∂–µ–Ω–∏—è:
–í–æ–ª–Ω–æ–≤–æ–º—É —É—Ä–∞–≤–Ω–µ–Ω–∏—é —É–¥–æ–≤–ª–µ—Ç–≤–æ—Ä—è–µ—Ç –≤–æ–ª–Ω–∞ –Ω–∞–ø—Ä—è–∂—ë–Ω–Ω–æ—Å—Ç–∏ —ç–ª–µ–∫—Ç—Ä–∏—á–µ—Å–∫–æ–≥–æ (–∏–ª–∏ –º–∞–≥–Ω–∏—Ç–Ω–æ–≥–æ) –ø–æ–ª—è —Ç–∏–ø–∞
,
–≥–¥–µ - ¬Ý- –≤–æ–ª–Ω–æ–≤–æ–µ —á–∏—Å–ª–æ.
–ü—Ä–∏ –ø–µ—Ä–µ—Ö–æ–¥–µ –≤ –∏–Ω–µ—Ä—Ü–∏–∞–ª—å–Ω—É—é —Å–∏—Å—Ç–µ–º—É, –¥–≤–∏–∂—É—â—É—é—Å—è —Å–æ —Å–∫–æ—Ä–æ—Å—Ç—å—é , –Ω–∞–±–ª—é–¥–∞–µ—Ç—Å—è –¥–æ–ø–ª–µ—Ä–æ–≤—Å–∫–∏–π —Å–¥–≤–∏–≥ —á–∞—Å—Ç–æ—Ç—ã.
–ü–æ–ø–µ—Ä–µ—á–Ω—ã–π —ç—Ñ—Ñ–µ–∫—Ç –î–æ–ø–ª–µ—Ä–∞, –∫–æ—Ç–æ—Ä—ã–π –æ–±—Å—É–∂–¥–∞–µ—Ç—Å—è –¥–æ—Å—Ç–∞—Ç–æ—á–Ω–æ –¥–∞–≤–Ω–æ, –¥–æ —Å–∏—Ö –ø–æ—Ä –Ω–µ –Ω–∞—à–µ–ª —Å–≤–æ–µ–≥–æ —É–≤–µ—Ä–µ–Ω–Ω–æ–≥–æ —ç–∫—Å–ø–µ—Ä–∏–º–µ–Ω—Ç–∞–ª—å–Ω–æ–≥–æ –ø–æ–¥—Ç–≤–µ—Ä–∂–¥–µ–Ω–∏—è. –î–ª—è –Ω–∞–±–ª—é–¥–µ–Ω–∏—è –∑–≤–µ–∑–¥—ã –∏–∑ –¥–≤–∏–∂—É—â–µ–π—Å—è –ò–°–û –Ω–µ–æ–±—Ö–æ–¥–∏–º–æ –Ω–∞–∫–ª–æ–Ω—è—Ç—å —Ç–µ–ª–µ—Å–∫–æ–ø –ø–æ —Ö–æ–¥—É –¥–≤–∏–∂–µ–Ω–∏—è –Ω–∞ —É–≥–æ–ª (2.26). –ó–≤–µ–∑–¥–∞, –Ω–∞–±–ª—é–¥–∞–µ–º–∞—è –≤ –∑–µ–Ω–∏—Ç–µ, –≤ –¥–µ–π—Å—Ç–≤–∏—Ç–µ–ª—å–Ω–æ—Å—Ç–∏ –Ω–∞—Ö–æ–¥–∏—Ç—Å—è –Ω–µ—Å–∫–æ–ª—å–∫–æ –ø–æ–∑–∞–¥–∏ –ø–æ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏—é –¥–≤–∏–∂–µ–Ω–∏—è. –ï–µ —É–≥–ª–æ–≤–æ–µ —Å–º–µ—â–µ–Ω–∏–µ –æ—Ç –≤–∏–¥–∏–º–æ–≥–æ –ø–æ–ª–æ–∂–µ–Ω–∏—è –ø—Ä–∏ —ç—Ç–æ–º –±—É–¥–µ—Ç –æ–ø—Ä–µ–¥–µ–ª—è—Ç—å—Å—è —Ç–æ–∂–µ (2.26). –ù–æ —ç—Ç–æ –±—É–¥–µ—Ç –æ–∑–Ω–∞—á–∞—Ç—å, —á—Ç–æ —Ç–∞–∫–∞—è –∑–≤–µ–∑–¥–∞ –ø–æ –æ—Ç–Ω–æ—à–µ–Ω–∏—é –∫ –Ω–∞–º –∏–º–µ–µ—Ç —Ä–∞–¥–∏–∞–ª—å–Ω—É—é —Å–æ—Å—Ç–∞–≤–ª—è—é—â—É—é —Å–∫–æ—Ä–æ—Å—Ç–∏, –æ–ø—Ä–µ–¥–µ–ª—è–µ–º—É—é —Å–æ–æ—Ç–Ω–æ—à–µ–Ω–∏–µ–º
.
–î–ª—è –º–∞–ª—ã—Ö —É–≥–ª–æ–≤ ,
, –∏ –¥–æ–ø–ª–µ—Ä–æ–≤—Å–∫–∏–π —Å–¥–≤–∏–≥ —á–∞—Å—Ç–æ—Ç—ã —Ä–∞–≤–µ–Ω
.¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý ¬Ý (2.27)
–î–∞–Ω–Ω—ã–π —Ä–µ–∑—É–ª—å—Ç–∞—Ç —á–∏—Å–ª–µ–Ω–Ω–æ —Å–æ–≤–ø–∞–¥–∞–µ—Ç —Å —Ä–µ–∑—É–ª—å—Ç–∞—Ç–∞–º–∏ –°–¢–û, –Ω–æ –ø—Ä–∏–Ω—Ü–∏–ø–∏–∞–ª—å–Ω–æ –æ—Ç–ª–∏—á–∞–µ—Ç—Å—è —Ç–µ–º, —á—Ç–æ –≤ –°–¢–û –ø–æ–ø–µ—Ä–µ—á–Ω—ã–π —ç—Ñ—Ñ–µ–∫—Ç –î–æ–ø–ª–µ—Ä–∞ (2.27) —Å—á–∏—Ç–∞–µ—Ç—Å—è —Ä–µ–∞–ª—å–Ω—ã–º, –∞ –≤ –¥–∞–Ω–Ω–æ–º —Å–ª—É—á–∞–µ —ç—Ç–æ —Ç–æ–ª—å–∫–æ –∫–∞–∂—É—â–∏–π—Å—è —ç—Ñ—Ñ–µ–∫—Ç.
3. –ó–∞–∫–ª—é—á–µ–Ω–∏–µ
–í —Å—Ç–∞—Ç—å–µ –ø–æ–ª—É—á–µ–Ω—ã –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è –ø–æ–ª–µ–π –ø—Ä–∏ –ø–µ—Ä–µ—Ö–æ–¥–µ –∏–∑ –æ–¥–Ω–æ–π –ò–°–û –≤ –¥—Ä—É–≥—É—é. –í –æ—Ç–ª–∏—á–∏–µ –æ—Ç –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏–π –õ–æ—Ä–µ–Ω—Ü–∞ –æ—Å–Ω–æ–≤–æ–π —Ç–∞–∫–∏—Ö –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏–π —è–≤–ª—è—é—Ç—Å—è –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è –ì–∞–ª–∏–ª–µ—è –∏ —Å–∏–º–º–µ—Ç—Ä–∏—á–Ω—ã–µ –∑–∞–∫–æ–Ω—ã –∏–Ω–¥—É–∫—Ü–∏–∏. –ü—Ä–∏ —ç—Ç–æ–º –∏—Å–ø–æ–ª—å–∑—É—é—Ç—Å—è –ø–æ–ª–Ω—ã–µ –ø—Ä–æ–∏–∑–≤–æ–¥–Ω—ã–µ, —É—á–∏—Ç—ã–≤–∞—é—â–∏–µ –∫–æ–Ω–≤–µ–∫—Ç–∏–≤–Ω—É—é –∏—Ö —á–∞—Å—Ç—å. –≠—Ç–æ –¥–∞–ª–æ –≤–æ–∑–º–æ–∂–Ω–æ—Å—Ç—å –æ–±—ä—è—Å–Ω–∏—Ç—å —è–≤–ª–µ–Ω–∏–µ —Ñ–∞–∑–æ–≤–æ–π –∞–±–µ—Ä—Ä–∞—Ü–∏–∏ —Å–≤–µ—Ç–∞ –∏ –≤—ã—è—Å–Ω–∏—Ç—å –ø—Ä–∏—á–∏–Ω—ã –ø–æ–ø–µ—Ä–µ—á–Ω–æ–≥–æ —ç—Ñ—Ñ–µ–∫—Ç–∞ –î–æ–ø–ª–µ—Ä–∞, –∫–æ—Ç–æ—Ä—ã–π —è–≤–ª—è–µ—Ç—Å—è —Ç–æ–ª—å–∫–æ –∫–∞–∂—É—â–∏–º—Å—è —ç—Ñ—Ñ–µ–∫—Ç–æ–º.
–õ–∏—Ç–µ—Ä–∞—Ç—É—Ä–∞
1. Petr Beckmann, Peter Mendics. Test of the Constancy of the Velocity of Electromagnetic Radiation in High Vacuum. RADIO SCIENCE Journal of Research NBS/USNC-URSI, v. 69D, No.4, April 1965.
2. De-Sitter W. Ein astronomischer Beweis fur die Konstanz der Lichtgeschwindigkeit // Physikalisch Zeitschrift.-1913. B.14. S.429; S. 1267-1268.¬Ý
3. Majorana Q. Experimental demonstration of the constancy of velocity of light emitted by a moving source // Lincei Rendues. 1918, v.27, pp. 402 - 406; Physical Review. 1918. v. 11, pp. 411 - 420; Philosophical Magazine. 1919, v. 37, pp. 145 - 150.¬Ý
4. Wallace Kantor . Direct First-Order Experiment on the Propagation of Light from a Moving Source . Journal of the Optical Society of America, 1962, v.52, Issue 9, pp. 978-984.
5. Ray O. Waddoups, W. Farrell Edwards, and John J. Merrill. Experimental Investigation of the Second Postulate of Special Relativity. Journal of the Optical Society of America, 1965, v.55, Issue 2, pp. 142-143.
6. Farley F., Kjellman J., Wallin J. Test of the second postulate relativity in the GeV region, Physical Letters, 1964, v. 12, No. 3, pp. 260 -262.
7. Fillipas T. A., Fox J. G. Velocity of gamma rays from a moving source, Physical Review. 1964, v. 135, pp. 1071 - 1075.¬Ý
8. Babcock G. C., Bergman T. G. Determination of the constancy of the speed of light // Journal of Optical Society of America. - 1964. - v. 54. No. 2. ‚Äì pp. 147 - 151.¬Ý
9. Fox J. G. Experimental Evidence for the Second Postulate of Special Relativity. American Journal of Physics, v. 30, 297 (1962).
10. Albert A. Michelson, Edward W. Morley. On the Relative Motion of the Earth and the Luminiferous Ether. The American Journal of Science. III series. Vol. XXII, No. 128, p.120¬Ý- 129.
11. F. F. Mende, Mende Interferometer with the Mechanical Division of the Ray. International Journal of Physics, vol. 5, no. 6 (2017): 197-200. doi: 10.12691/ijp-5-6-1.
12. F. F. Mende. Mende Interferometer: From the Experimental Refutation of the Lorentz Transformations and the Principles of the Invariance of the Speed of Light to New Prospects for the Development of Passive Radar, Global Journal of Frontier Research: F, Volume 117, Issue 5, Version 1. 2017.
13. –§. –§. –ú–µ–Ω–¥–µ. –ö –≤–æ–ø—Ä–æ—Å—É –æ–± —É—Ç–æ—á–Ω–µ–Ω–∏–∏ —É—Ä–∞–≤–Ω–µ–Ω–∏–π —ç–ª–µ–∫—Ç—Ä–æ–º–∞–≥–Ω–∏—Ç–Ω–æ–π –∏–Ω–¥—É–∫—Ü–∏–∏. –•–∞—Ä—å–∫–æ–≤, –¥–µ–ø–æ–Ω–∏—Ä–æ–≤–∞–Ω–∞ –≤ –í–ò–ù–ò–¢–ò, ‚Ññ774-–í88 –î–µ–ø., 1988, 32—Å.
14. –§. –§. –ú–µ–Ω–¥–µ. –°—É—â–µ—Å—Ç–≤—É—é—Ç –ª–∏ –æ—à–∏–±–∫–∏ –≤ —Å–æ–≤—Ä–µ–º–µ–Ω–Ω–æ–π —Ñ–∏–∑–∏–∫–µ. –•–∞—Ä—å–∫–æ–≤: –ö–æ–Ω—Å—Ç–∞–Ω—Ç–∞, 2003.
15. F. F. Mende. On refinement of certain laws of classical electrodynamics. arXiv, physics/0402084.
16. –§. –§. –ú–µ–Ω–¥–µ. –ù–æ–≤—ã–µ –ø–æ–¥—Ö–æ–¥—ã –≤ —Å–æ–≤—Ä–µ–º–µ–Ω–Ω–æ–π –∫–ª–∞—Å—Å–∏—á–µ—Å–∫–æ–π —ç–ª–µ–∫—Ç—Ä–æ–¥–∏–Ω–∞–º–∏–∫–µ. –ß–∞—Å—Ç—å I. –ò–Ω–∂–µ–Ω–µ—Ä–Ω–∞—è —Ñ–∏–∑–∏–∫–∞, 2013, ‚Ññ1, —Å. 35-49.20. –§. –§. –ú–µ–Ω–¥–µ,
17. –§. –§. –ú–µ–Ω–¥–µ. –ù–æ–≤—ã–µ –ø–æ–¥—Ö–æ–¥—ã –≤ —Å–æ–≤—Ä–µ–º–µ–Ω–Ω–æ–π –∫–ª–∞—Å—Å–∏—á–µ—Å–∫–æ–π —ç–ª–µ–∫—Ç—Ä–æ–¥–∏–Ω–∞–º–∏–∫–µ, –ß–∞—Å—Ç—å II. –ò–Ω–∂–µ–Ω–µ—Ä–Ω–∞—è —Ñ–∏–∑–∏–∫–∞, 2013, ‚Ññ2, —Å. 3-17.
18. F. F. Mende, Concept of Scalar-Vector Potential in the Contemporary Electrodynamic, Problem of Homopolar Induction and Its Solution. International Journal of Physics, 2014, Vol. 2, No. 6, p. 202-210.
URL:http://pubs.sciepub.com/ijp/2/6/4
19. F. F. Mende, Consideration and the Refinement of Some Laws and Concepts of Classical Electrodynamics and New Ideas in Modern Electrodynamics. International Journal of Physics, 2014, Vol. 2, No. 8, p. 231-263.
URL: http://pubs.sciepub.com/ijp/2/6/8
20. F. F. Mende. Concept of Scalar-Vector Potential and Its Experimental Confirmation. AASCIT Journal of Physics, 2015, Vol.1, No. 3, p. 135-148.
URL: http://www.aascit.org/journal/archive2?journalId=977&paperId=2176
21. –§. –§. –ú–µ–Ω–¥–µ. –ù–æ–≤–∞—è —ç–ª–µ–∫—Ç—Ä–æ–¥–∏–Ω–∞–º–∏–∫–∞. –Ý–µ–≤–æ–ª—é—Ü–∏—è –≤ —Å–æ–≤—Ä–µ–º–µ–Ω–Ω–æ–π —Ñ–∏–∑–∏–∫–µ. –•–∞—Ä—å–∫–æ–≤: –ù–¢–ú–¢, 2012.
22. F. F. Mende. Classical Relativistic Corrections to Coulomb Law. AASCIT Journal of Physics, 2015, Vol.1, No. 2, p. 69-75.
23. F. F. Mende. The Classical Conversions of Electromagnetic Fields on Their Consequences. AASCIT Journal of Physics, 2015, Vol.1, No. 1, p. 11-18.
URL: http://www.aascit.org/journal/archive2?journalId=977&paperId=1647
–§. –§. –ú–µ–Ω–¥–µ
–£–∫—Ä–∞–∏–Ω–∞, –•–∞—Ä—å–∫–æ–≤
fedormende@gmail.com